36 Officers Problem – Part 2

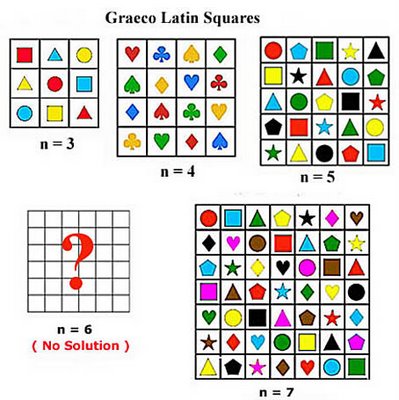
The great mathematician Euler (1707-1783) was an authority on magic squares and did a considerable amount of work on Latin Squares and Graeco Latin squares. He even came up with methods for constructing them. But he could never produce a Graeco Latin Square of the order 6. (n=6). This led him to state the famous “ 36 Officers Problem”. It goes like this.

“ Is it possible to arrange six regiments, each consisting of six officers of different ranks, in such a way that that no row or column contains two or more officers from the same regiment or with the same rank.” This simply meant can you construct a Latin-Graeco Square of order 6 ?”

The above is a diagrammatic colorful representation of some of the solutions for Latin-Graeco squares starting from n=3 to n=9. The squares of n = 8 and n = 9 was based on the method of construction by Bose.