36 OFFICERS PROBLEM - Part 3

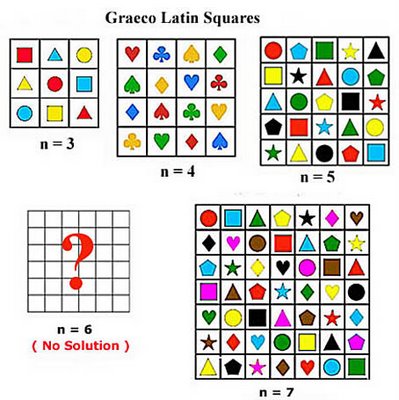
In Part 2, we annunciated Euler’s “36 Officers Problem. In spite of much experimentation, he was unable to discover a Latin-Graeco square of order 6. He was also unable to prove that it did not exist. He therefore made the famous conjecture, which meant that:



“ There does not exist such a Latin-Graeco Square whose order has the form
n = 4k + 2 ”

In the first case of k = 0: n=2 is trivially impossible. The next case k = 1: n=6 is, according to Euler’s conjecture, impossible and so also cases where n= 10, 14,18, 22,26 …. etc are impossible. This conjecture went unsolved for over 100 years. In1900, a French mathematician, Gaston Terry checked every possible combination for a 6 x 6 Euler square and showed that none existed, partly proving Euler’s conjecture.

Finally in 1960, Bose, Shrikhande and Parker managed to prove that Euler squares (i.e. Latin-Graeco squares) exist for all orders except for n=6. (and obviously form=2)

The Euler Square which is shown on the left where n = 10, which for 177 years had been believed to be impossible was finally constructed by Parker in 1960.Here in each column and in each row each color of the outer square and each colour of the inner square occurs only once. No combination of 2 colours occurs twice.

36 Officers Problem – Part 2

The great mathematician Euler (1707-1783) was an authority on magic squares and did a considerable amount of work on Latin Squares and Graeco Latin squares. He even came up with methods for constructing them. But he could never produce a Graeco Latin Square of the order 6. (n=6). This led him to state the famous “ 36 Officers Problem”. It goes like this.

“ Is it possible to arrange six regiments, each consisting of six officers of different ranks, in such a way that that no row or column contains two or more officers from the same regiment or with the same rank.” This simply meant can you construct a Latin-Graeco Square of order 6 ?”

The above is a diagrammatic colorful representation of some of the solutions for Latin-Graeco squares starting from n=3 to n=9. The squares of n = 8 and n = 9 was based on the method of construction by Bose.

36 OFFICERS PROBLEM - Part 1

In my recently designed game www.sodokogame.com I mentioned Euler’s “36 officers problem” as the driving force. In this article I propose to say a little bit more without using Combinatorial Mathematics, as I too have difficulty in grasping this. I will explain by means of necessary diagrams.

First we must know what is a LATIN square and what is a Graeco-Latin square ( also referred to as Euler squares ) as the latter was the basis of the “36 Officers Problem” .

A LATIN square is an n x n table filled with n different symbols in such a way that each occurs exactly once in each row and exactly once in each column.

A GRAECO-LATIN square is also an n x n table, each cell of which contains a PAIR of symbols, composed of a symbol from each of 2 sets of n elements. Each PAIR occurs exactly once in the table. Each SYMBOL in the 2 sets occurs exactly once in each row and exactly once in each column. Another way of defining is as follows. When two Latin squares are constructed, one with Latin letters and one with Greek letters, in such a way that when superposed, each Latin letter appears once and only once with each Greek letter, the resulting square is called a Graeco-Latin square.

In the image above we see 2 LATIN squares and 1 GRAECO-LATIN square in letters and below I have represented them in colors, for easy understanding and that is the manner I will use for the remainder of this article.